Servicios al cliente
Sobre nosotros
Copyright © 2025 Desertcart Holdings Limited
Desert Online General Trading LLC
Dubai, United Arab Emirates
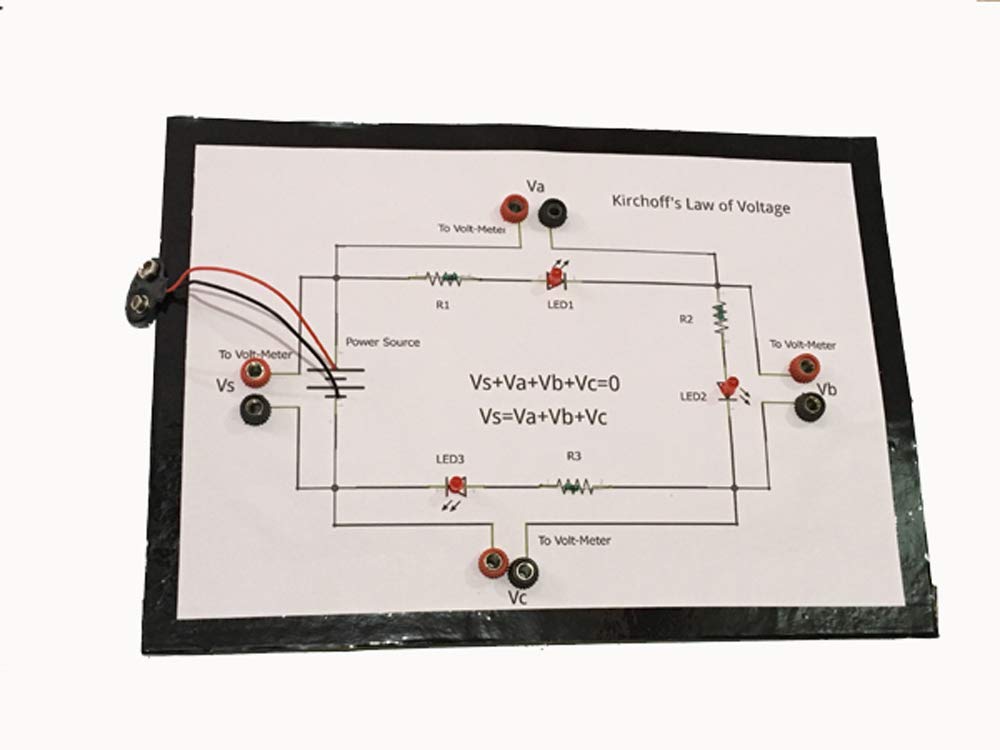

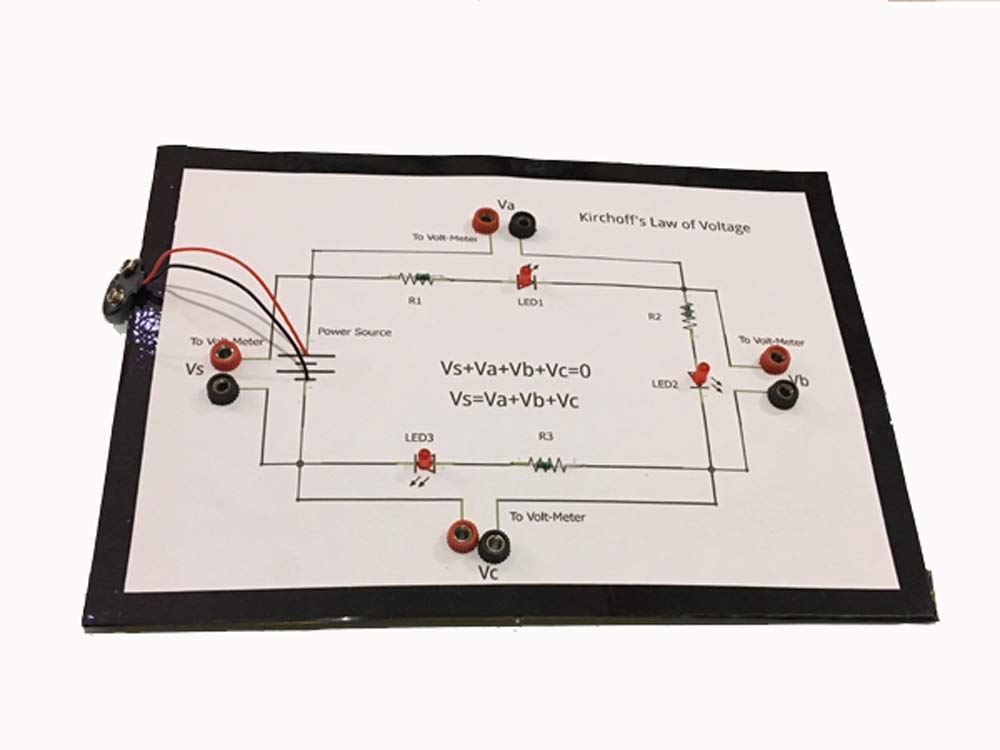
Project Hub� -Kirchhoff's Law of Voltage (KVL) Mesh Analysis || Science Physics / Electricity Educational Kit(Base-Cardboard)
Trustpilot
Hace 1 mes
Hace 1 semana